Logistic Regression Modeling with Cross Validation on Word Frequecy¶
As we have seen from the previous notebook, topic probabilities of reviews do not have good predictive powers of customers’ ratings of restaurants. Thus, in this notebook, we investigate how multinomial logistic regression performs. We will calculate the TF-IDF statistics from the reviews and use them to predict customers’ ratings.
Part 1: load dependencies and read data¶
In [1]:
import pandas as pd
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.feature_selection import SelectKBest,chi2
import numpy as np
from sklearn.model_selection import KFold
from sklearn.linear_model import LogisticRegression
import unittest
import matplotlib.pyplot as plt
import re
import scipy.sparse
import random
In [2]:
# set the seed
random.seed(259)
In [3]:
# load the data
review = pd.read_csv("data/reviews.csv")
Part 2: Term Frequency - Inverse Document Frequenc (TF-IDF) Transformation¶
TF-IDF means “Term Frequency - Inverse Document Frequency”. It is a powerful technique to detect important words in a collection of documents. “Term Frequency” (TF) meansures the frequency of word \(w_i\) in document \(d_j\), and the “Inverse Document Frequency” (IDF) measures how much information the word provides, i.e., the frequency of word \(w_i\) in the collection of documents. The TF-IDF value for a word \(w_i\) in document \(d_j\) is positively associated with word frequencies and negatively associated with document frequencies. The math formula for TF-IDF is:
And IDF can be smoothed using the formula:
where \(N\) is the number of documents considered and \(n_i\) is the frequency of \(w_i\) in the all documents considered.
In this project, TF-IDF is used in logistic regression classification. In the following analysis, we did several steps to fit the best logistic regression model:
- constructed the TF-IDF matrix,
- used \(\chi^2\) independent test to select top \(1,000\) keywords from training set,
- computed the TF-IDF values of the \(1,000\) keywords,
- splited the whole dataset into training set and validation set using 10-fold cross-valudation,
- used the TF-IDF values as covariates, the star values of review (ratings) as responses, to build a logistic regression model in the training set,
- tried 3 different tuning parameters respectively,
- applied the models built in training set to validation set and obtained the predicted star values for each tuning parameter,
- computed the Mean Squared Error (MSE) between true star value and predicted star value in validation set,
- and chose the optimal tuning parameters which produces lowest MSE.
construct the TF-IDF matrix¶
In [4]:
# make raw dataset into the format for TF-idf transformation
star = np.array(review.stars)
text = list(map(lambda x: x[2:-1].replace("\\n","\n"), review.text))
pat = re.compile(r"[^\w\s]")
text_clean = np.array(list(map(lambda x: pat.sub(" ",x).lower(), text)))
# create TF-IDF
vectorizer = TfidfVectorizer(stop_words = "english")
text_features = vectorizer.fit_transform(text_clean)
vocab = vectorizer.get_feature_names()
# save
scipy.sparse.save_npz('result/text_features.npz', text_features)
np.save('result/star', star)
In [5]:
print("Number of observations in the text_features dataset is", text_features.shape[0],
"\nNumber of covariates in the text_features dataset is", text_features.shape[1])
Number of observations in the text_features dataset is 60222
Number of covariates in the text_features dataset is 50137
In [6]:
print("The format of text_feature is\n", text_features[-1:])
print("The format of star is\n", star)
The format of text_feature is
(0, 17785) 0.060146376659
(0, 19534) 0.0664307345244
(0, 37080) 0.0971322128585
(0, 6868) 0.215221170104
(0, 41758) 0.14424586198
(0, 16242) 0.115560138128
(0, 3668) 0.169463104229
(0, 33687) 0.18134186701
(0, 42347) 0.244903534338
(0, 30214) 0.173935675158
(0, 19663) 0.219337002949
(0, 10430) 0.210710863093
(0, 38753) 0.253060975895
(0, 11918) 0.548103837493
(0, 1483) 0.283007805783
(0, 2376) 0.371248887227
(0, 43674) 0.274472118608
The format of star is
[2 4 5 ..., 4 5 5]
Part 3: Compute MSE¶
Write a function to compute step 2 to 8¶
In [7]:
def compute_CV_mse(df_text, df_star, n_fold, n_words, seed, parameters):
"""Return the Mean Squared Error (MSE) between predictied reponses and true responses in validation set.
Parameters
----------
df_text: TF-IDF format sparse matrix
df_star: array of responses in logistic model
n_fold: number of folds in cross-validation, positive integer
n_words: number of keywords selected, positive integer
seed: random seed for splitting training and validation set
parameters: tuning parameters of logistic regression, positive float vector
Return
------
Array
A numeric Array where each value in dimension 0 is the tuning parameter,
and each value in dimension 1 is MSE computed using the corresponding tuning parameter
Example
-------
>>> text_features = vectorizer.fit_transform(text_clean)
... star = np.array(review.stars)
... compute_CV_mse(text_features, star, 2, 10, 1, (100.0, 1000.0))
"""
# parameters must be positive
test = False
if isinstance(n_fold, int):
test = True
else:
raise TypeError("n_fold is not an integer")
if n_fold > 0:
test = True
else:
raise ValueError("n_fold should be positive")
if isinstance(n_words, int):
test = True
else:
raise TypeError("n_words is not an integer")
if n_words > 0:
test = True
else:
raise ValueError("n_words should be positive")
for i in parameters:
if i > 0:
test = True
else:
raise ValueError("parameters should be positive")
# create K-folds
kf = KFold(n_fold, shuffle = True, random_state = seed)
# create empty dataframe
mse = np.zeros([n_fold + 1, len(parameters)])
k = 0
for train_idx,val_idx in kf.split(df_text):
# create training and validation sets
text_features_train = df_text[train_idx]
text_features_val = df_text[val_idx]
star_train = df_star[train_idx]
star_val = df_star[val_idx]
# using $chi^2$ independent test to select top 1,000 keywords from training set
fselect = SelectKBest(chi2, k = n_words)
# transform training set to format that fits select functuon
text_features_train = fselect.fit_transform(text_features_train, star_train)
text_features_val = text_features_val[:, fselect.get_support()]
# compute MSE for each parameter
t = 0
for para in parameters:
# logistic regression with C = parameter,
# where C is positive float, indicates "Inverse of regularization strength",
# and smaller values specify stronger regularization.
mod_temp = LogisticRegression(C = para)
# fit regression on training set
mod_temp.fit(X = text_features_train, y = star_train)
# predict star values on validation set
pred = mod_temp.predict(X = text_features_val)
# compute MSE as a dataframe, each value is one mse in one validation set
mse[k,t] = sum((pred - star_val)**2)/len(pred)
t+= 1
k+= 1
# compute overall MSE
mse_out = np.mean(mse[1:n_fold,], axis = 0)
return(np.vstack((parameters, mse_out)))
Execute the function¶
compute MSE with 10 fold cross-validation, of first 1,000 keywords, with random splitting seed for training and validation sets = 1, and original tuning parameters = (1, 100, 1000, 10000, 100000).
NOTE: Original tuning parameter range is [1, 100,000], the current range [10, 100] is selected after many trails as the optimal range of tuning parameters**
In [8]:
# output
para, mse = compute_CV_mse(df_text = text_features, df_star = star, n_fold = 10,
n_words = 1000, seed = 1, parameters = list(range(10, 110, 10)))
In [9]:
d = {'parameters' : pd.Series(para),
'mse' : pd.Series(mse)}
df = pd.DataFrame(d)
df_sorted = df.sort_values(by=['mse'])
df_sorted.to_hdf('result/df_sorted.h5', 'df_sorted')
print("Sorted MSE and corresponding parameters: small to big")
df_sorted
Sorted MSE and corresponding parameters: small to big
Out[9]:
| mse | parameters | |
|---|---|---|
| 4 | 0.748335 | 50.0 |
| 3 | 0.749202 | 40.0 |
| 1 | 0.749553 | 20.0 |
| 2 | 0.749811 | 30.0 |
| 5 | 0.749885 | 60.0 |
| 6 | 0.750014 | 70.0 |
| 7 | 0.751435 | 80.0 |
| 8 | 0.753058 | 90.0 |
| 0 | 0.753077 | 10.0 |
| 9 | 0.753630 | 100.0 |
Choose tuning parameters with minimum mse, and we get:
In [9]:
print("The minimum MSE is", np.round(df_sorted.iloc[0][0], 4), "with tuning parameter =", df_sorted.iloc[0][1])
The minimum MSE is 0.7483 with tuning parameter = 50.0
Plot MSE for different tuning parameters
In [10]:
df.plot(x = 'parameters', y = "mse")
plt.title("Cross-validation MSE by tuning parameters \nin multinomial logistic regression")
plt.savefig("fig/mse_logistic.png")
plt.show()
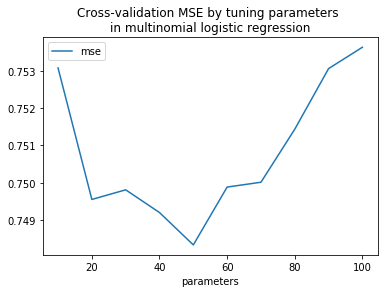
We observe that the multinomial logistic regression performs reasonably well. The cross-validated mean square error (MSE) is 0.748. It means that TF-IDF statistics from the reviews have explanatory and predictive powers of customers’ ratings of restaurants.
Part 4: Testing¶
In [11]:
def test_n_words_positive():
"""Test that when n_words is negative, raise value error"""
# YOUR CODE HERE
try:
compute_CV_mse(df_text = text_features, df_star = star, n_fold = 2,
n_words = -1, seed = 1, parameters = 10.0**np.arange(0,2))
except ValueError:
assert True
else:
assert False
def test_n_words_integer():
"""Test that when n_words is negative, raise value error"""
# YOUR CODE HERE
try:
compute_CV_mse(df_text = text_features, df_star = star, n_fold = 2,
n_words = "f", seed = 1, parameters = 10.0**np.arange(0,2))
except TypeError:
assert True
else:
assert False
def test_n_folds_positive():
"""Test that when n_words is negative, raise value error"""
# YOUR CODE HERE
try:
compute_CV_mse(df_text = text_features, df_star = star, n_fold = -2,
n_words = 1, seed = 1, parameters = 10.0**np.arange(0,2))
except ValueError:
assert True
else:
assert False
def test_n_folds_integer():
"""Test that when n_words is negative, raise value error"""
# YOUR CODE HERE
try:
compute_CV_mse(df_text = text_features, df_star = star, n_fold = "f",
n_words = 2, seed = 1, parameters = 10.0**np.arange(0,2))
except TypeError:
assert True
else:
assert False
def test_parameters_positive():
"""Test that when n_words is negative, raise value error"""
# YOUR CODE HERE
try:
compute_CV_mse(df_text = text_features, df_star = star, n_fold = 2,
n_words = 1, seed = 1, parameters = (-1,-3))
except ValueError:
assert True
else:
assert False
In [12]:
test_n_words_positive()
test_n_words_integer()
test_n_folds_positive()
test_n_folds_integer()